This Jupyter notebook can be downloaded from time_a_pulsar.ipynb, or viewed as a python script at time_a_pulsar.py.
Time a pulsar
This notebook walks through a simple pulsar timing session, as one might do with TEMPO/TEMPO2: load a .par file, load a .tim file, do a fit, plot the residuals before and after. This one also displays various additional information you might find useful, and also ignores but then plots TOAs with large uncertainties. Similar code is available as a standalone script at fit_NGC6440E.py
[1]:
import astropy.units as u
import matplotlib.pyplot as plt
import pint.fitter
from pint.models import get_model_and_toas
from pint.residuals import Residuals
import pint.logging
pint.logging.setup(level="INFO")
[1]:
1
We want to load a parameter file and some TOAs. For the purposes of this notebook, we’ll load in ones that are included with PINT; the pint.config.examplefile() calls return the path to where those files are in the PINT distribution. If you wanted to use your own files, you would probably know their filenames and could just set parfile="myfile.par" and timfile="myfile.tim".
[2]:
import pint.config
parfile = pint.config.examplefile("NGC6440E.par")
timfile = pint.config.examplefile("NGC6440E.tim")
Let’s load the par and tim files. We could load them separately with the get_model and get_TOAs functions, but the parfile may contain information about how to interpret the TOAs, so it is convenient to load the two together so that the TOAs take into account details in the par file.
[3]:
m, t_all = get_model_and_toas(parfile, timfile)
m
[3]:
TimingModel(
AbsPhase(
MJDParameter( TZRMJD 53801.3860512007484954 (d) frozen=True),
strParameter( TZRSITE 1 frozen=True),
floatParameter( TZRFRQ 1949.609 (MHz) frozen=True)),
AstrometryEquatorial(
MJDParameter( POSEPOCH 53750.0000000000000000 (d) frozen=True),
floatParameter( PX 0.0 (mas) frozen=True),
AngleParameter( RAJ 17:48:52.75000000 (hourangle) +/- 0h00m00.05s frozen=False),
AngleParameter( DECJ -20:21:29.00000000 (deg) +/- 0d00m00.4s frozen=False),
floatParameter( PMRA 0.0 (mas / yr) frozen=True),
floatParameter( PMDEC 0.0 (mas / yr) frozen=True)),
DispersionDM(
floatParameter( DM 223.9 (pc / cm3) +/- 0.3 pc / cm3 frozen=False),
floatParameter( DM1 UNSET,
MJDParameter( DMEPOCH UNSET),
SolarSystemShapiro(
boolParameter( PLANET_SHAPIRO N frozen=True)),
SolarWindDispersion(
floatParameter( NE_SW 0.0 (1 / cm3) frozen=True),
floatParameter( NE_SW1 0.0 (1 / (yr cm3)) frozen=True),
MJDParameter( SWEPOCH UNSET,
floatParameter( SWP 2.0 () frozen=True),
intParameter( SWM 0 frozen=True)),
Spindown(
floatParameter( F0 61.485476554 (Hz) +/- 5e-10 Hz frozen=False),
MJDParameter( PEPOCH 53750.0000000000000000 (d) frozen=True),
floatParameter( F1 -1.181e-15 (Hz / s) +/- 1e-18 Hz / s frozen=False)),
TroposphereDelay(
boolParameter( CORRECT_TROPOSPHERE N frozen=True))
)
There are many messages here. As a rule messages marked INFO can safely be ignored, they are simply informational; take a look at them if something unexpected happens. Messages marked WARNING or ERROR are more serious. (These messages are emitted by the python logger module and can be suppressed or written to a log file if they are annoying.)
Let’s just print out a quick summary.
[4]:
t_all.print_summary()
Number of TOAs: 62
Number of commands: 0
Number of observatories: 1 ['gbt']
MJD span: 53478.286 to 54187.587
Date span: 2005-04-18 06:51:39.290648106 to 2007-03-28 14:05:44.808308037
gbt TOAs (62):
Min freq: 1549.609 MHz
Max freq: 2212.109 MHz
Min error: 13.2 us
Max error: 118 us
Median error: 22.1 us
[5]:
rs = Residuals(t_all, m).phase_resids
xt = t_all.get_mjds()
plt.figure()
plt.plot(xt, rs, "x")
plt.title(f"{m.PSR.value} Pre-Fit Timing Residuals")
plt.xlabel("MJD")
plt.ylabel("Residual (phase)")
plt.grid()
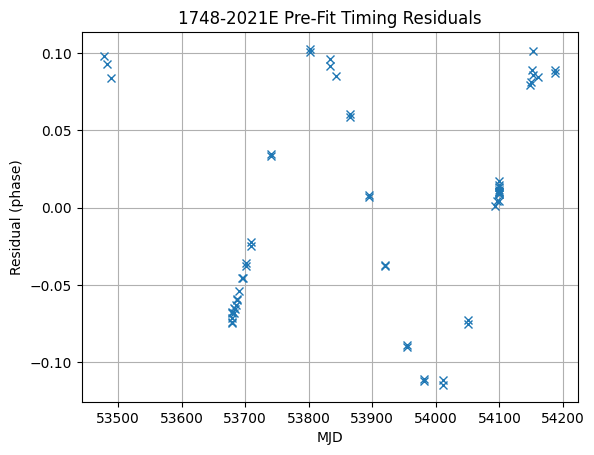
We could proceed immediately to fitting the par file, but some of those uncertainties seem a little large. Let’s discard the data points with uncertainties \(>30\,\mu\text{s}\) - uncertainty estimation is not always reliable when the signal-to-noise is low.
[6]:
error_ok = t_all.table["error"] <= 30 * u.us
t = t_all[error_ok]
t.print_summary()
Number of TOAs: 44
Number of commands: 0
Number of observatories: 1 ['gbt']
MJD span: 53478.286 to 54187.587
Date span: 2005-04-18 06:51:39.290648106 to 2007-03-28 14:05:44.808308037
gbt TOAs (44):
Min freq: 1724.609 MHz
Max freq: 1949.609 MHz
Min error: 13.2 us
Max error: 29.9 us
Median error: 21.5 us
[7]:
rs = Residuals(t, m).phase_resids
xt = t.get_mjds()
plt.figure()
plt.plot(xt, rs, "x")
plt.title(f"{m.PSR.value} Pre-Fit Timing Residuals")
plt.xlabel("MJD")
plt.ylabel("Residual (phase)")
plt.grid()
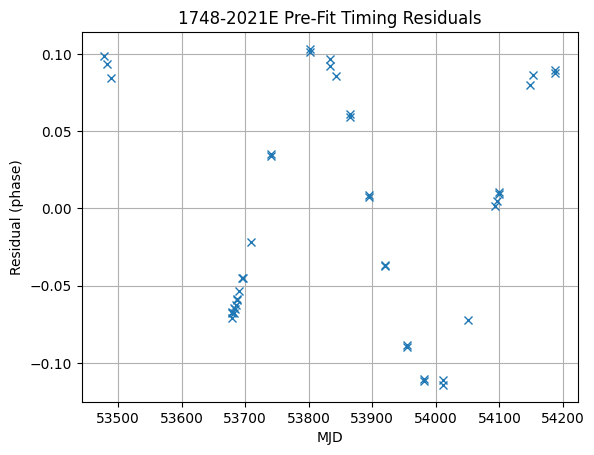
Now let’s fit the par file to the residuals, using the auto function to pick the right fitter for our data.
[8]:
f = pint.fitter.Fitter.auto(t, m)
f.fit_toas()
[9]:
# Print some basic params
print("Best fit has reduced chi^2 of", f.resids.chi2_reduced)
print("RMS in phase is", f.resids.phase_resids.std())
print("RMS in time is", f.resids.time_resids.std().to(u.us))
Best fit has reduced chi^2 of 1.0367399180607070475
RMS in phase is 0.0011179201241166127
RMS in time is 18.181856708577673 us
[10]:
# Show the parameter correlation matrix
corm = f.get_parameter_correlation_matrix(pretty_print=True)
Parameter correlation matrix:
RAJ DECJ F0 F1 DM
RAJ 1.000
DECJ -0.047 1.000
F0 -0.105 0.250 1.000
F1 0.277 -0.323 -0.773 1.000
DM 0.139 0.054 -0.099 0.030 1.000
[11]:
f.print_summary()
Fitted model using downhill_wls method with 5 free parameters to 44 TOAs
Prefit residuals Wrms = 1113.6432896435356 us, Postfit residuals Wrms = 18.17566589789211 us
Chisq = 39.396 for 38 d.o.f. for reduced Chisq of 1.037
PAR Prefit Postfit Units
=================== ==================== ============================ =====
PSR 1748-2021E 1748-2021E None
EPHEM DE421 DE421 None
CLOCK TT(BIPM2019) TT(BIPM2019) None
UNITS TDB TDB None
START 53478.3 d
FINISH 54187.6 d
TIMEEPH FB90 FB90 None
T2CMETHOD IAU2000B IAU2000B None
DILATEFREQ N None
DMDATA N None
NTOA 0 None
CHI2 39.3961
CHI2R 1.03674
TRES 18.1757 us
POSEPOCH 53750 d
PX 0 mas
RAJ 17h48m52.75s 17h48m52.80032123s +/- 0.00014 hourangle_second
DECJ -20d21m29s -20d21m29.39582205s +/- 0.034 arcsec
PMRA 0 mas / yr
PMDEC 0 mas / yr
F0 61.4855 61.485476554374(18) Hz
PEPOCH 53750 d
F1 -1.181e-15 -1.1817(15)×10⁻¹⁵ Hz / s
TZRMJD 53801.4 d
TZRSITE 1 1 None
TZRFRQ 1949.61 MHz
CORRECT_TROPOSPHERE N None
PLANET_SHAPIRO N None
NE_SW 0 1 / cm3
NE_SW1 0 1 / (yr cm3)
SWP 2
SWM 0 None
DM 223.9 224.07(8) pc / cm3
Derived Parameters:
Period = 0.016264003404376±0.000000000000005 s
Pdot = (3.126±0.004)×10⁻¹⁹
Characteristic age = 8.244e+08 yr (braking index = 3)
Surface magnetic field = 2.28e+09 G
Magnetic field at light cylinder = 4882 G
Spindown Edot = 2.868e+33 erg / s (I=1e+45 cm2 g)
[12]:
plt.figure()
plt.errorbar(
xt.value,
f.resids.time_resids.to(u.us).value,
t.get_errors().to(u.us).value,
fmt="x",
)
plt.title(f"{m.PSR.value} Post-Fit Timing Residuals")
plt.xlabel("MJD")
plt.ylabel("Residual (us)")
plt.grid()
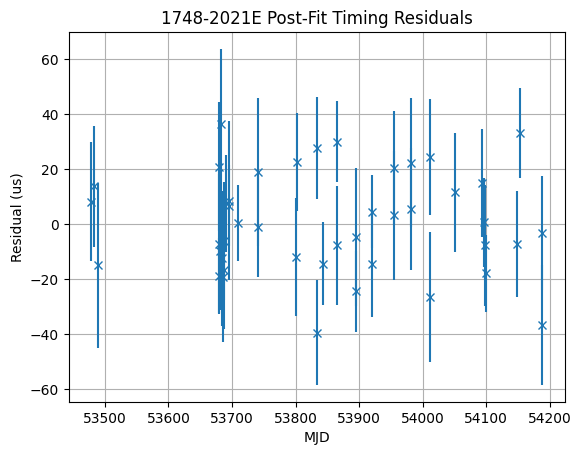
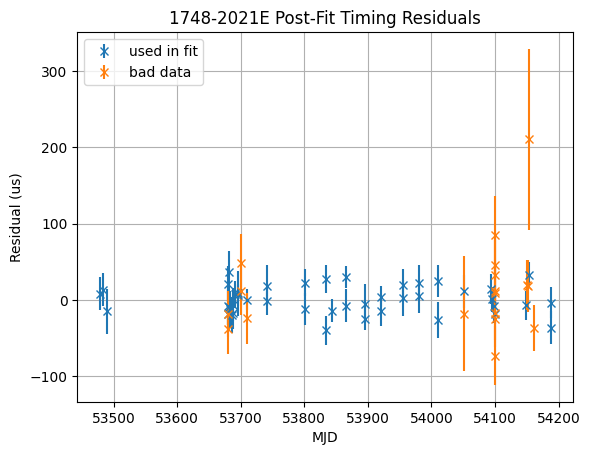
[13]:
t_bad = t_all[~error_ok]
r_bad = Residuals(t_bad, f.model)
plt.figure()
plt.errorbar(
xt.value,
f.resids.time_resids.to(u.us).value,
t.get_errors().to(u.us).value,
fmt="x",
label="used in fit",
)
plt.errorbar(
t_bad.get_mjds().value,
r_bad.time_resids.to(u.us).value,
t_bad.get_errors().to(u.us).value,
fmt="x",
label="bad data",
)
plt.title(f"{m.PSR.value} Post-Fit Timing Residuals")
plt.xlabel("MJD")
plt.ylabel("Residual (us)")
plt.grid()
plt.legend(loc="upper left")
[13]:
<matplotlib.legend.Legend at 0x7fca5f0ec450>
[14]:
plt.show()
[15]:
f.model.write_parfile("/tmp/output.par", "wt")
print(f.model.as_parfile())
# Created: 2024-12-18T17:15:17.507796
# PINT_version: 0+untagged.722.g91be315
# User: docs
# Host: build-26631508-project-85767-nanograv-pint
# OS: Linux-5.19.0-1028-aws-x86_64-with-glibc2.35
# Python: 3.11.10 (main, Nov 5 2024, 16:13:19) [GCC 11.4.0]
# Format: pint
# read_time: 2024-12-18T17:15:13.810292
# allow_tcb: False
# convert_tcb: False
# allow_T2: False
# original_name: /home/docs/checkouts/readthedocs.org/user_builds/nanograv-pint/envs/stable/lib/python3.11/site-packages/pint/data/examples/NGC6440E.par
PSR 1748-2021E
EPHEM DE421
CLK TT(BIPM2019)
UNITS TDB
START 53478.2858714195382639
FINISH 54187.5873241702319097
TIMEEPH FB90
T2CMETHOD IAU2000B
DILATEFREQ N
DMDATA N
NTOA 44
CHI2 39.39611688630687
CHI2R 1.036739918060707
TRES 18.175665897892110156
RAJ 17:48:52.80032123 1 0.00013868970124516315
DECJ -20:21:29.39582205 1 0.03403292479973890616
PMRA 0.0
PMDEC 0.0
PX 0.0
POSEPOCH 53750.0000000000000000
F0 61.48547655437361534 1 1.8413563782587741397e-11
F1 -1.1816723614839368656e-15 1 1.4578585393661638702e-18
PEPOCH 53750.0000000000000000
TZRMJD 53801.3860512007484954
TZRSITE 1
TZRFRQ 1949.609
CORRECT_TROPOSPHERE N
PLANET_SHAPIRO N
SOLARN0 0.0
NE_SW1 0.0
SWM 0
DM 224.06649954592670423 1 0.0827222664478675096