This Jupyter notebook can be downloaded from MCMC_walkthrough.ipynb, or viewed as a python script at MCMC_walkthrough.py.

MCMC Walkthrough

This notebook contains examples of how to use the MCMC Fitter class and how to modify it for more specific uses.

All of these examples will use the EmceeSampler class, which is currently the only Sampler implementation supported by PINT. Future work may include implementations of other sampling methods.

import random
import numpy as np
import pint.models
import pint.toa as toa
import pint.fermi_toas as fermi
from pint.residuals import Residuals
from pint.sampler import EmceeSampler
from pint.mcmc_fitter import MCMCFitter, MCMCFitterBinnedTemplate
from pint.scripts.event_optimize import read_gaussfitfile, marginalize_over_phase
import pint.config
import pint.logging
import matplotlib.pyplot as plt
import pickle

pint.logging.setup("WARNING")

2

np.random.seed(0)
state = np.random.mtrand.RandomState()

Basic Example

This example will show a vanilla, unmodified MCMCFitter operating with a simple template and on a small dataset. The sampler is a wrapper around the emcee package, so it requires a number of walkers for the ensemble sampler. This number of walkers must be specified by the user.

The first few lines are the basic methods used to load in models, TOAs, and templates. More detailed information on this can be found in pint.scripts.event_optimize.py.

parfile = pint.config.examplefile("PSRJ0030+0451_psrcat.par")
eventfile = pint.config.examplefile(
    "J0030+0451_P8_15.0deg_239557517_458611204_ft1weights_GEO_wt.gt.0.4.fits"
)
gaussianfile = pint.config.examplefile("templateJ0030.3gauss")
weightcol = "PSRJ0030+0451"

minWeight = 0.9
nwalkers = 10
# make this larger for real use
nsteps = 50
nbins = 256
phs = 0.0

model = pint.models.get_model(parfile)
ts = fermi.get_Fermi_TOAs(
    eventfile, weightcolumn=weightcol, minweight=minWeight, ephem="DE421"
)
# Introduce a small error so that residuals can be calculated
ts.table["error"] = 1.0
ts.filename = eventfile
ts.compute_TDBs()
ts.compute_posvels(ephem="DE421", planets=False)

weights, _ = ts.get_flag_value("weight", as_type=float)
template = read_gaussfitfile(gaussianfile, nbins)
template /= template.mean()

Sampler and Fitter creation

The sampler must be initialized first, and then passed as an argument into the MCMCFitter constructor. The fitter will send its log-posterior probabilility function to the sampler for the MCMC run. The log-prior and log-likelihood functions of the MCMCFitter can be written by the user. The default behavior is to use the functions implemented in the pint.mcmc_fitter module.

The EmceeSampler requires only an argument for the number of walkers in the ensemble.

Here, we use MCMCFitterBinnedTemplate because the Gaussian template not a callable function. If the template is analytic and callable, then MCMCFitterAnalyticTemplate should be used, and template parameters can be used in the optimization.

sampler = EmceeSampler(nwalkers)

fitter = MCMCFitterBinnedTemplate(
    ts, model, sampler, template=template, weights=weights, phs=phs
)
fitter.sampler.random_state = state

The next step determines the predicted starting phase of the pulse, which is used to set an accurate initial phase in the model. This will result in a more accurate fit, although we don’t actually use it here. This step uses the marginalize over phase method implemented in pint.scripts.event_optimize.py.

phases = fitter.get_event_phases()
maxbin, like_start = marginalize_over_phase(
    phases, template, weights=fitter.weights, minimize=True, showplot=True
)
phase = 1.0 - maxbin[0] / float(len(template))
print(f"Starting pulse likelihood: {like_start}")
print(f"Starting pulse phase: {phase}")
print("Pre-MCMC Values:")
for name, val in zip(fitter.fitkeys, fitter.fitvals):
    print("%8s:\t%12.5g" % (name, val))

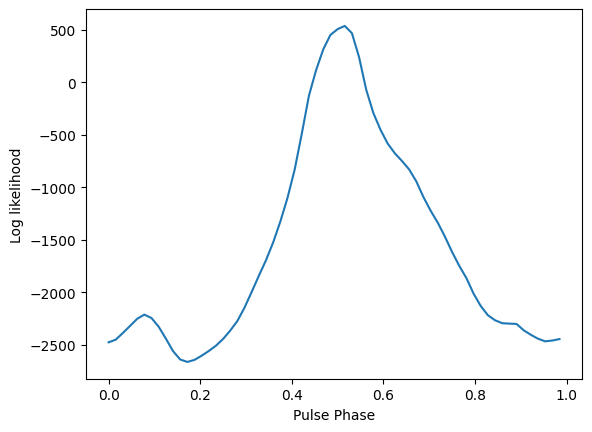
Starting pulse likelihood: 539.5465827007408
Starting pulse phase: 0.5147440486522087
Pre-MCMC Values:
      F0:             205.53
      F1:        -4.2976e-16

The MCMCFitter class is a subclass of pint.fitter.Fitter. It is run in exactly the same way - with the fit_toas() method.

fitter.fit_toas(maxiter=nsteps, pos=None)
fitter.set_parameters(fitter.maxpost_fitvals)

You must install the tqdm library to use progress indicators with emcee

To make this run relatively fast for demonstration purposes, nsteps was purposefully kept very small. However, this means that the results of this fit will not be very good. For an example of MCMC fitting that produces better results, look at pint/examples/fitNGC440E_MCMC.py

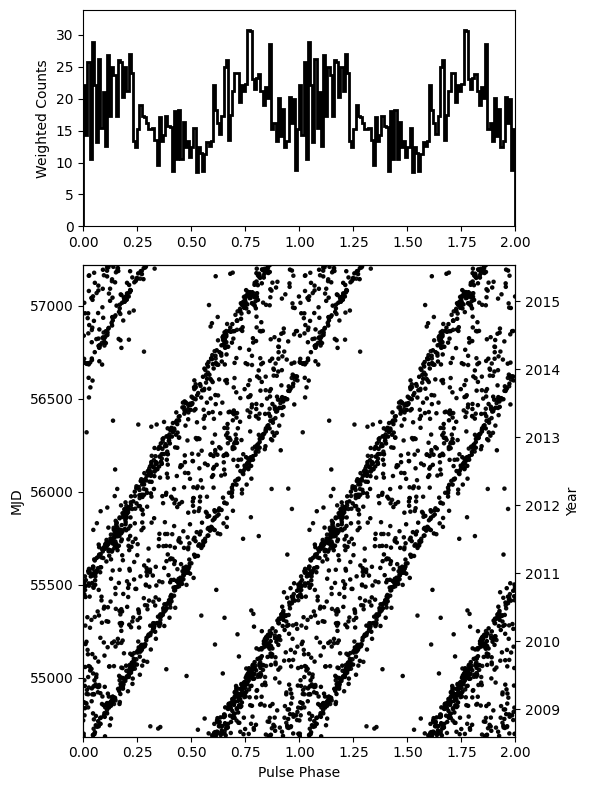
fitter.phaseogram()
samples = np.transpose(sampler.sampler.get_chain(discard=10), (1, 0, 2)).reshape(
    (-1, fitter.n_fit_params)
)
ranges = map(
    lambda v: (v[1], v[2] - v[1], v[1] - v[0]),
    zip(*np.percentile(samples, [16, 50, 84], axis=0)),
)
print("Post-MCMC values (50th percentile +/- (16th/84th percentile):")
for name, vals in zip(fitter.fitkeys, ranges):
    print("%8s:" % name + "%25.15g (+ %12.5g  / - %12.5g)" % vals)
print("Final ln-posterior: %12.5g" % fitter.lnposterior(fitter.maxpost_fitvals))

Post-MCMC values (50th percentile +/- (16th/84th percentile):
      F0:         205.530699280042 (+   9.0885e-09  / -   1.1338e-08)
      F1:    -4.29740012337748e-16 (+   5.1682e-20  / -   5.3725e-20)
Final ln-posterior:      -1082.6

Customizable Example

This second example will demonstrate how the MCMCFitter can be customized for more involved use. Users can define their own prior and likelihood probability functions to allow for more unique configurations.

timfile2 = pint.config.examplefile("NGC6440E.tim")
parfile2 = pint.config.examplefile("NGC6440E.par.good")
model2 = pint.models.get_model(parfile2)
toas2 = toa.get_TOAs(timfile2, planets=False, ephem="DE421")
nwalkers2 = 12
nsteps2 = 10

The new probability functions must be defined by the user and must have the following characteristics. They must take two arguments: an MCMCFitter object, and a vector of fitting parameters (called theta here). They must return a float (not an astropy.Quantity).

The new functions can be passed to the constructor of the MCMCFitter object using the keywords lnprior and lnlike, as shown below.

def lnprior_basic(ftr, theta):
    lnsum = 0.0
    for val, key in zip(theta[:-1], ftr.fitkeys[:-1]):
        lnsum += getattr(ftr.model, key).prior_pdf(val, logpdf=True)
    return lnsum


def lnlikelihood_chi2(ftr, theta):
    ftr.set_parameters(theta)
    # Uncomment to view progress
    # print('Count is: %d' % ftr.numcalls)
    return -Residuals(toas=ftr.toas, model=ftr.model).chi2


sampler2 = EmceeSampler(nwalkers=nwalkers2)
fitter2 = MCMCFitter(
    toas2, model2, sampler2, lnprior=lnprior_basic, lnlike=lnlikelihood_chi2
)
fitter2.sampler.random_state = state

like_start = fitter2.lnlikelihood(fitter2, fitter2.get_parameters())
print(f"Starting pulse likelihood: {like_start}")

Starting pulse likelihood: -59.57510595134

fitter2.fit_toas(maxiter=nsteps2, pos=None)

You must install the tqdm library to use progress indicators with emcee

18.359665882555686316

samples2 = np.transpose(sampler2.sampler.get_chain(), (1, 0, 2)).reshape(
    (-1, fitter2.n_fit_params)
)
ranges2 = map(
    lambda v: (v[1], v[2] - v[1], v[1] - v[0]),
    zip(*np.percentile(samples2, [16, 50, 84], axis=0)),
)
print("Post-MCMC values (50th percentile +/- (16th/84th percentile):")
for name, vals in zip(fitter2.fitkeys, ranges2):
    print("%8s:" % name + "%25.15g (+ %12.5g  / - %12.5g)" % vals)
print("Final ln-posterior: %12.5g" % fitter2.lnposterior(fitter2.maxpost_fitvals))

Post-MCMC values (50th percentile +/- (16th/84th percentile):
     RAJ:         17.8146667648213 (+   6.3569e-09  / -   6.9211e-09)
    DECJ:        -20.3581627407672 (+   2.0255e-06  / -   3.5102e-06)
      F0:         61.4854765543732 (+   9.7415e-12  / -    4.853e-12)
      F1:    -1.18140566547566e-15 (+   5.2028e-19  / -   7.1514e-19)
      DM:         224.112791617016 (+    0.0065565  / -    0.0078194)
Final ln-posterior:        18.36