This Jupyter notebook can be downloaded from rednoise-fit-example.ipynb, or viewed as a python script at rednoise-fit-example.py.
Red noise and DM noise fitting examples
This notebook provides an example on how to fit for red noise and DM noise using PINT using simulated datasets.
We will use the PLRedNoise and PLDMNoise models to generate noise realizations (these models provide Fourier Gaussian process descriptions of achromatic red noise and DM noise respectively).
We will fit the generated datasets using the WaveX and DMWaveX models, which provide deterministic Fourier representations of achromatic red noise and DM noise respectively.
Finally, we will convert the WaveX/DMWaveX amplitudes into spectral parameters and compare them with the injected values.
[1]:
from pint import DMconst
from pint.models import get_model
from pint.simulation import make_fake_toas_uniform
from pint.logging import setup as setup_log
from pint.fitter import WLSFitter
from pint.utils import (
dmwavex_setup,
find_optimal_nharms,
wavex_setup,
plrednoise_from_wavex,
pldmnoise_from_dmwavex,
)
from io import StringIO
import numpy as np
import astropy.units as u
from matplotlib import pyplot as plt
from copy import deepcopy
setup_log(level="WARNING")
[1]:
1
Red noise fitting
Simulation
The first step is to generate a simulated dataset for demonstration. Note that we are adding PHOFF as a free parameter. This is required for the fit to work properly.
[2]:
par_sim = """
PSR SIM3
RAJ 05:00:00 1
DECJ 15:00:00 1
PEPOCH 55000
F0 100 1
F1 -1e-15 1
PHOFF 0 1
DM 15 1
TNREDAMP -13
TNREDGAM 3.5
TNREDC 30
TZRMJD 55000
TZRFRQ 1400
TZRSITE gbt
UNITS TDB
EPHEM DE440
CLOCK TT(BIPM2019)
"""
m = get_model(StringIO(par_sim))
[3]:
# Now generate the simulated TOAs.
ntoas = 2000
toaerrs = np.random.uniform(0.5, 2.0, ntoas) * u.us
freqs = np.linspace(500, 1500, 8) * u.MHz
t = make_fake_toas_uniform(
startMJD=53001,
endMJD=57001,
ntoas=ntoas,
model=m,
freq=freqs,
obs="gbt",
error=toaerrs,
add_noise=True,
add_correlated_noise=True,
name="fake",
include_bipm=True,
include_gps=True,
multi_freqs_in_epoch=True,
)
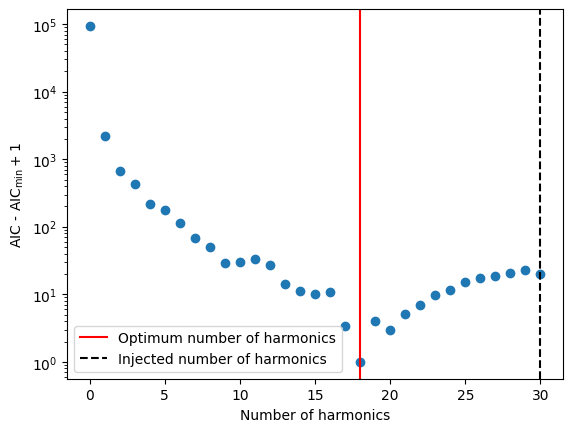
Optimal number of harmonics
The optimal number of harmonics can be estimated by minimizing the Akaike Information Criterion (AIC). This is implemented in the pint.utils.find_optimal_nharms function.
[4]:
m1 = deepcopy(m)
m1.remove_component("PLRedNoise")
nharm_opt, d_aics = find_optimal_nharms(m1, t, "WaveX", 30)
print("Optimum no of harmonics = ", nharm_opt)
Optimum no of harmonics = 18
[5]:
print(np.argmin(d_aics))
18
[6]:
# The Y axis is plotted in log scale only for better visibility.
plt.scatter(list(range(len(d_aics))), d_aics + 1)
plt.axvline(nharm_opt, color="red", label="Optimum number of harmonics")
plt.axvline(
int(m.TNREDC.value), color="black", ls="--", label="Injected number of harmonics"
)
plt.xlabel("Number of harmonics")
plt.ylabel("AIC - AIC$_\\min{} + 1$")
plt.legend()
plt.yscale("log")
# plt.savefig("sim3-aic.pdf")
[7]:
# Now create a new model with the optimum number of harmonics
m2 = deepcopy(m1)
Tspan = t.get_mjds().max() - t.get_mjds().min()
wavex_setup(m2, T_span=Tspan, n_freqs=nharm_opt, freeze_params=False)
ftr = WLSFitter(t, m2)
ftr.fit_toas(maxiter=10)
m2 = ftr.model
print(m2)
# Created: 2024-04-26T18:13:50.797391
# PINT_version: 1.0
# User: docs
# Host: build-24199856-project-85767-nanograv-pint
# OS: Linux-5.19.0-1028-aws-x86_64-with-glibc2.35
# Python: 3.11.6 (main, Feb 1 2024, 16:47:41) [GCC 11.4.0]
# Format: pint
PSR SIM3
EPHEM DE440
CLOCK TT(BIPM2019)
UNITS TDB
START 53000.9999999567009723
FINISH 56985.0000000464666667
DILATEFREQ N
DMDATA N
NTOA 2000
CHI2 1978.8923392722775
CHI2R 1.011186683327684
TRES 0.9957052309807108302
RAJ 4:59:59.99993822 1 0.00011573598793788619
DECJ 15:00:00.00830633 1 0.01198851904110715891
PMRA 0.0
PMDEC 0.0
PX 0.0
F0 99.99999999999973407 1 5.481555924589841595e-13
F1 -1.0001885866558731608e-15 1 1.8396897465349361956e-19
PEPOCH 55000.0000000000000000
TZRMJD 55000.0000000000000000
TZRSITE gbt
TZRFRQ 1400.0
PHOFF 7.97446950225684e-06 1 0.000919203388902604
PLANET_SHAPIRO N
DM 15.000005361532816695 1 4.8034934434404951204e-06
WXEPOCH 55000.0000000000000000
WXFREQ_0001 0.00025100401605860164
WXSIN_0001 -8.473465449785957e-06 1 6.147940534078539e-07
WXCOS_0001 9.402765417886073e-06 1 1.1113778205776333e-05
WXFREQ_0002 0.0005020080321172033
WXSIN_0002 3.3627677677776185e-06 1 3.111389390714105e-07
WXCOS_0002 -1.280325985009055e-06 1 2.8245190068496112e-06
WXFREQ_0003 0.000753012048175805
WXSIN_0003 -9.361363598007033e-07 1 2.1619506995660663e-07
WXCOS_0003 2.16819701121508e-06 1 1.2955275014674381e-06
WXFREQ_0004 0.0010040160642344066
WXSIN_0004 -3.028818112451145e-07 1 1.7167920943983864e-07
WXCOS_0004 -1.130597762533114e-06 1 7.627361387155268e-07
WXFREQ_0005 0.0012550200802930083
WXSIN_0005 2.127365652793034e-07 1 1.5057491150691667e-07
WXCOS_0005 5.664113033950716e-07 1 5.200685467426483e-07
WXFREQ_0006 0.00150602409635161
WXSIN_0006 3.242141102315289e-07 1 1.3934621278630993e-07
WXCOS_0006 -2.707046399473845e-08 1 3.972557116397403e-07
WXFREQ_0007 0.0017570281124102117
WXSIN_0007 -7.474139478529634e-08 1 1.3904977345336267e-07
WXCOS_0007 3.333726962659463e-07 1 3.3369211599164954e-07
WXFREQ_0008 0.002008032128468813
WXSIN_0008 -1.4329800828044916e-07 1 1.513350401065759e-07
WXCOS_0008 -5.334913196940198e-07 1 3.1099691784191285e-07
WXFREQ_0009 0.002259036144527415
WXSIN_0009 -1.2322327432403508e-07 1 1.8800849614320336e-07
WXCOS_0009 2.7513481932837313e-08 1 3.35981726604075e-07
WXFREQ_0010 0.0025100401605860165
WXSIN_0010 6.410026563192522e-08 1 3.283909749994486e-07
WXCOS_0010 -3.110527639026382e-07 1 5.122231783196616e-07
WXFREQ_0011 0.002761044176644618
WXSIN_0011 5.129386548237054e-07 1 2.7024954465016724e-06
WXCOS_0011 -2.5358528401321297e-06 1 3.7089028176466886e-06
WXFREQ_0012 0.00301204819270322
WXSIN_0012 -6.630788840577341e-08 1 1.9722104639031887e-07
WXCOS_0012 1.9742731296708015e-07 1 2.3726914087225834e-07
WXFREQ_0013 0.0032630522087618214
WXSIN_0013 2.5882544894505178e-08 1 9.260698067138624e-08
WXCOS_0013 -5.253205969007666e-09 1 1.002079479641346e-07
WXFREQ_0014 0.0035140562248204233
WXSIN_0014 -5.439424422474702e-08 1 6.01719503793267e-08
WXCOS_0014 5.140988330316192e-09 1 5.966473663557866e-08
WXFREQ_0015 0.003765060240879025
WXSIN_0015 2.1979318313170547e-08 1 4.636304115045937e-08
WXCOS_0015 -2.0562629722881777e-08 1 4.4858134204494466e-08
WXFREQ_0016 0.004016064256937626
WXSIN_0016 1.2093378396045494e-07 1 4.007068648850346e-08
WXCOS_0016 -6.515225663891393e-09 1 3.8141729628065e-08
WXFREQ_0017 0.004267068272996228
WXSIN_0017 9.25684505298751e-08 1 3.579041563750877e-08
WXCOS_0017 -4.09061877575761e-08 1 3.591213153505012e-08
WXFREQ_0018 0.00451807228905483
WXSIN_0018 7.157894410934828e-08 1 3.4463793054581903e-08
WXCOS_0018 2.587507856196089e-09 1 3.4575753173523416e-08
Estimating the spectral parameters from the WaveX fit.
[8]:
# Get the Fourier amplitudes and powers and their uncertainties.
idxs = np.array(m2.components["WaveX"].get_indices())
a = np.array([m2[f"WXSIN_{idx:04d}"].quantity.to_value("s") for idx in idxs])
da = np.array([m2[f"WXSIN_{idx:04d}"].uncertainty.to_value("s") for idx in idxs])
b = np.array([m2[f"WXCOS_{idx:04d}"].quantity.to_value("s") for idx in idxs])
db = np.array([m2[f"WXCOS_{idx:04d}"].uncertainty.to_value("s") for idx in idxs])
print(len(idxs))
P = (a**2 + b**2) / 2
dP = ((a * da) ** 2 + (b * db) ** 2) ** 0.5
f0 = (1 / Tspan).to_value(u.Hz)
fyr = (1 / u.year).to_value(u.Hz)
18
[9]:
# We can create a `PLRedNoise` model from the `WaveX` model.
# This will estimate the spectral parameters from the `WaveX`
# amplitudes.
m3 = plrednoise_from_wavex(m2)
print(m3)
# Created: 2024-04-26T18:13:50.843379
# PINT_version: 1.0
# User: docs
# Host: build-24199856-project-85767-nanograv-pint
# OS: Linux-5.19.0-1028-aws-x86_64-with-glibc2.35
# Python: 3.11.6 (main, Feb 1 2024, 16:47:41) [GCC 11.4.0]
# Format: pint
PSR SIM3
EPHEM DE440
CLOCK TT(BIPM2019)
UNITS TDB
START 53000.9999999567009723
FINISH 56985.0000000464666667
DILATEFREQ N
DMDATA N
NTOA 2000
CHI2 1978.8923392722775
CHI2R 1.011186683327684
TRES 0.9957052309807108302
RAJ 4:59:59.99993822 1 0.00011573598793788619
DECJ 15:00:00.00830633 1 0.01198851904110715891
PMRA 0.0
PMDEC 0.0
PX 0.0
F0 99.99999999999973407 1 5.481555924589841595e-13
F1 -1.0001885866558731608e-15 1 1.8396897465349361956e-19
PEPOCH 55000.0000000000000000
TZRMJD 55000.0000000000000000
TZRSITE gbt
TZRFRQ 1400.0
PHOFF 7.97446950225684e-06 1 0.000919203388902604
TNREDAMP -13.068454810244567 0 0.1504043838287556
TNREDGAM 3.929020588541497 0 0.5061023436214108
TNREDC 18.0
PLANET_SHAPIRO N
DM 15.000005361532816695 1 4.8034934434404951204e-06
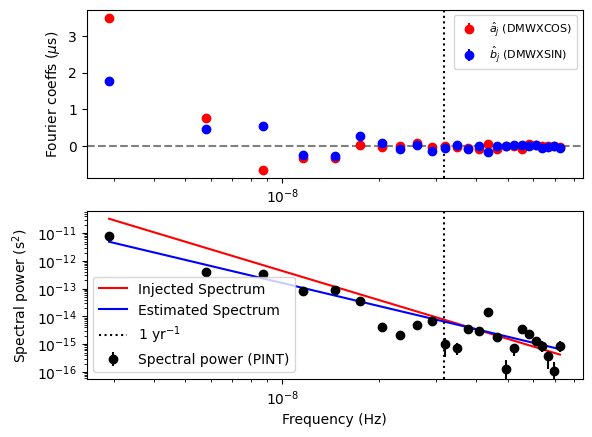
[10]:
# Now let us plot the estimated spectrum with the injected
# spectrum.
plt.subplot(211)
plt.errorbar(
idxs * f0,
b * 1e6,
db * 1e6,
ls="",
marker="o",
label="$\\hat{a}_j$ (WXCOS)",
color="red",
)
plt.errorbar(
idxs * f0,
a * 1e6,
da * 1e6,
ls="",
marker="o",
label="$\\hat{b}_j$ (WXSIN)",
color="blue",
)
plt.axvline(fyr, color="black", ls="dotted")
plt.axhline(0, color="grey", ls="--")
plt.ylabel("Fourier coeffs ($\mu$s)")
plt.xscale("log")
plt.legend(fontsize=8)
plt.subplot(212)
plt.errorbar(
idxs * f0, P, dP, ls="", marker="o", label="Spectral power (PINT)", color="k"
)
P_inj = m.components["PLRedNoise"].get_noise_weights(t)[::2][:nharm_opt]
plt.plot(idxs * f0, P_inj, label="Injected Spectrum", color="r")
P_est = m3.components["PLRedNoise"].get_noise_weights(t)[::2][:nharm_opt]
print(len(idxs), len(P_est))
plt.plot(idxs * f0, P_est, label="Estimated Spectrum", color="b")
plt.xscale("log")
plt.yscale("log")
plt.ylabel("Spectral power (s$^2$)")
plt.xlabel("Frequency (Hz)")
plt.axvline(fyr, color="black", ls="dotted", label="1 yr$^{-1}$")
plt.legend()
18 18
[10]:
<matplotlib.legend.Legend at 0x7f8b12612290>
Note the outlier in the 1 year^-1 bin. This is caused by the covariance with RA and DEC, which introduce a delay with the same frequency.
DM noise fitting
Let us now do a similar kind of analysis for DM noise.
[11]:
par_sim = """
PSR SIM4
RAJ 05:00:00 1
DECJ 15:00:00 1
PEPOCH 55000
F0 100 1
F1 -1e-15 1
PHOFF 0 1
DM 15 1
TNDMAMP -13
TNDMGAM 3.5
TNDMC 30
TZRMJD 55000
TZRFRQ 1400
TZRSITE gbt
UNITS TDB
EPHEM DE440
CLOCK TT(BIPM2019)
"""
m = get_model(StringIO(par_sim))
[12]:
# Generate the simulated TOAs.
ntoas = 2000
toaerrs = np.random.uniform(0.5, 2.0, ntoas) * u.us
freqs = np.linspace(500, 1500, 8) * u.MHz
t = make_fake_toas_uniform(
startMJD=53001,
endMJD=57001,
ntoas=ntoas,
model=m,
freq=freqs,
obs="gbt",
error=toaerrs,
add_noise=True,
add_correlated_noise=True,
name="fake",
include_bipm=True,
include_gps=True,
multi_freqs_in_epoch=True,
)
[13]:
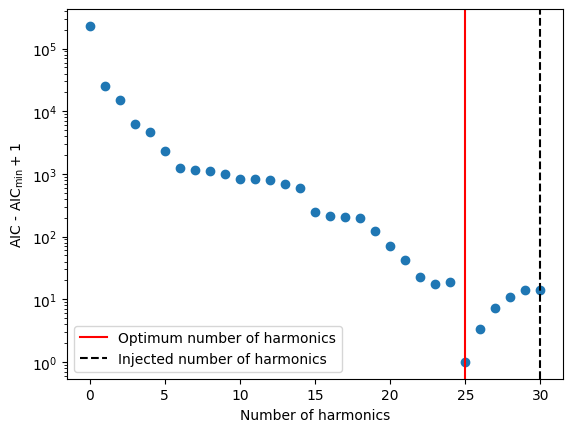
# Find the optimum number of harmonics by minimizing AIC.
m1 = deepcopy(m)
m1.remove_component("PLDMNoise")
m2 = deepcopy(m1)
nharm_opt, d_aics = find_optimal_nharms(m2, t, "DMWaveX", 30)
print("Optimum no of harmonics = ", nharm_opt)
Optimum no of harmonics = 29
[14]:
# The Y axis is plotted in log scale only for better visibility.
plt.scatter(list(range(len(d_aics))), d_aics + 1)
plt.axvline(nharm_opt, color="red", label="Optimum number of harmonics")
plt.axvline(
int(m.TNDMC.value), color="black", ls="--", label="Injected number of harmonics"
)
plt.xlabel("Number of harmonics")
plt.ylabel("AIC - AIC$_\\min{} + 1$")
plt.legend()
plt.yscale("log")
# plt.savefig("sim3-aic.pdf")
[15]:
# Now create a new model with the optimum number of
# harmonics
m2 = deepcopy(m1)
Tspan = t.get_mjds().max() - t.get_mjds().min()
dmwavex_setup(m2, T_span=Tspan, n_freqs=nharm_opt, freeze_params=False)
ftr = WLSFitter(t, m2)
ftr.fit_toas(maxiter=10)
m2 = ftr.model
print(m2)
# Created: 2024-04-26T18:15:16.719950
# PINT_version: 1.0
# User: docs
# Host: build-24199856-project-85767-nanograv-pint
# OS: Linux-5.19.0-1028-aws-x86_64-with-glibc2.35
# Python: 3.11.6 (main, Feb 1 2024, 16:47:41) [GCC 11.4.0]
# Format: pint
PSR SIM4
EPHEM DE440
CLOCK TT(BIPM2019)
UNITS TDB
START 53000.9999999566649306
FINISH 56985.0000000461960185
DILATEFREQ N
DMDATA N
NTOA 2000
CHI2 1857.424900754861
CHI2R 0.9599095094340367
TRES 0.97162572601109028586
RAJ 4:59:59.99999813 1 0.00000189187880060054
DECJ 15:00:00.00005795 1 0.00016094659501375309
PMRA 0.0
PMDEC 0.0
PX 0.0
F0 99.99999999999995441 1 3.6172376841794999413e-14
F1 -9.999997374756911203e-16 1 8.3063805585857470247e-22
PEPOCH 55000.0000000000000000
TZRMJD 55000.0000000000000000
TZRSITE gbt
TZRFRQ 1400.0
PHOFF 0.0008532562142660407 1 5.485044809139759e-06
PLANET_SHAPIRO N
DM 15.000002844181466291 1 4.9639686941126820373e-06
DMWXEPOCH 55000.0000000000000000
DMWXFREQ_0001 0.00025100401605861633
DMWXSIN_0001 -0.0002555316933051208 1 6.0494919897969605e-06
DMWXCOS_0001 0.0020977009881442935 1 6.844327519232588e-06
DMWXFREQ_0002 0.0005020080321172327
DMWXSIN_0002 0.00017095406480681236 1 4.739349254096964e-06
DMWXCOS_0002 0.001044940460460309 1 4.6246859325217945e-06
DMWXFREQ_0003 0.000753012048175849
DMWXSIN_0003 -1.958487079069422e-05 1 4.4912512687705445e-06
DMWXCOS_0003 0.0005680055738656053 1 4.465899058368525e-06
DMWXFREQ_0004 0.0010040160642344653
DMWXSIN_0004 -0.0004323862484827116 1 4.498254761764577e-06
DMWXCOS_0004 0.00039317418235939645 1 4.369022441718683e-06
DMWXFREQ_0005 0.0012550200802930816
DMWXSIN_0005 3.423838440654048e-06 1 4.505866991722764e-06
DMWXCOS_0005 3.832475461772822e-05 1 4.3200860491175225e-06
DMWXFREQ_0006 0.001506024096351698
DMWXSIN_0006 -4.7039041379081234e-05 1 4.450973432508634e-06
DMWXCOS_0006 -8.977999067452258e-06 1 4.359914744600429e-06
DMWXFREQ_0007 0.0017570281124103142
DMWXSIN_0007 -4.784410912726731e-05 1 4.484330811822235e-06
DMWXCOS_0007 -7.4407359323908465e-06 1 4.291589698821464e-06
DMWXFREQ_0008 0.0020080321284689307
DMWXSIN_0008 -3.344666933566975e-05 1 4.3498425442497185e-06
DMWXCOS_0008 -8.459466868108835e-05 1 4.376152634204027e-06
DMWXFREQ_0009 0.002259036144527547
DMWXSIN_0009 3.874568316528602e-05 1 4.419108018473933e-06
DMWXCOS_0009 3.663460285438021e-05 1 4.322607671890699e-06
DMWXFREQ_0010 0.002510040160586163
DMWXSIN_0010 5.495459278979398e-05 1 4.486493021704261e-06
DMWXCOS_0010 3.714533774230447e-05 1 4.319162044023476e-06
DMWXFREQ_0011 0.00276104417664478
DMWXSIN_0011 -2.3575221052498582e-05 1 6.9650811690325e-06
DMWXCOS_0011 2.209531579468559e-05 1 6.925527796419467e-06
DMWXFREQ_0012 0.003012048192703396
DMWXSIN_0012 -2.845133182335025e-05 1 4.3406050896773686e-06
DMWXCOS_0012 2.7344399068380898e-05 1 4.3838910003763495e-06
DMWXFREQ_0013 0.0032630522087620122
DMWXSIN_0013 9.262359340564546e-06 1 4.361569167748246e-06
DMWXCOS_0013 -7.180497469765872e-06 1 4.3330228582334105e-06
DMWXFREQ_0014 0.0035140562248206285
DMWXSIN_0014 1.6487466459736234e-05 1 4.336071639855034e-06
DMWXCOS_0014 -4.340341715312522e-06 1 4.357461843775394e-06
DMWXFREQ_0015 0.0037650602408792447
DMWXSIN_0015 -1.823166403288984e-05 1 4.373531711335741e-06
DMWXCOS_0015 -1.2806108292741007e-05 1 4.319337889432894e-06
DMWXFREQ_0016 0.004016064256937861
DMWXSIN_0016 7.418268592731552e-06 1 4.375918130207522e-06
DMWXCOS_0016 -7.976132881317408e-06 1 4.311776052973161e-06
DMWXFREQ_0017 0.004267068272996478
DMWXSIN_0017 2.373968139774579e-05 1 4.44092560617799e-06
DMWXCOS_0017 -2.8134518881071866e-05 1 4.243254833934742e-06
DMWXFREQ_0018 0.004518072289055094
DMWXSIN_0018 1.4991261151906106e-05 1 4.340530639587386e-06
DMWXCOS_0018 -3.7403647700099926e-06 1 4.339302850026394e-06
DMWXFREQ_0019 0.00476907630511371
DMWXSIN_0019 1.603370859534752e-05 1 4.282121442311668e-06
DMWXCOS_0019 -3.5772340183646504e-06 1 4.3966121165398716e-06
DMWXFREQ_0020 0.005020080321172326
DMWXSIN_0020 -1.707503880032196e-05 1 4.328808634147451e-06
DMWXCOS_0020 -1.1947959418509529e-05 1 4.3434083298280186e-06
DMWXFREQ_0021 0.0052710843372309425
DMWXSIN_0021 2.0124231552590018e-05 1 4.354605889705174e-06
DMWXCOS_0021 -1.772329827220724e-06 1 4.3129373708134376e-06
DMWXFREQ_0022 0.00552208835328956
DMWXSIN_0022 -2.3350302776759263e-05 1 4.350912772762775e-06
DMWXCOS_0022 -1.599185458811154e-05 1 4.323817652100384e-06
DMWXFREQ_0023 0.005773092369348176
DMWXSIN_0023 -2.2134031920051017e-06 1 4.408316650826794e-06
DMWXCOS_0023 1.0299648087190312e-05 1 4.260607250496348e-06
DMWXFREQ_0024 0.006024096385406792
DMWXSIN_0024 -8.825943451774864e-06 1 4.441551523839238e-06
DMWXCOS_0024 3.391841839261316e-06 1 4.227249003905832e-06
DMWXFREQ_0025 0.006275100401465408
DMWXSIN_0025 -3.554269415718666e-06 1 4.358370101549827e-06
DMWXCOS_0025 3.853178190318557e-06 1 4.3069780326232565e-06
DMWXFREQ_0026 0.0065261044175240245
DMWXSIN_0026 6.4402924045132545e-06 1 4.369264093382938e-06
DMWXCOS_0026 -1.1687689454965374e-05 1 4.2852149371069535e-06
DMWXFREQ_0027 0.006777108433582641
DMWXSIN_0027 2.6599916086089604e-06 1 4.332383815174336e-06
DMWXCOS_0027 -8.46279171986668e-06 1 4.311891787009311e-06
DMWXFREQ_0028 0.007028112449641257
DMWXSIN_0028 1.0612905786627824e-05 1 4.287929989857072e-06
DMWXCOS_0028 -1.5238019838626781e-05 1 4.360868650832272e-06
DMWXFREQ_0029 0.007279116465699873
DMWXSIN_0029 6.606061965710876e-06 1 4.354919245279496e-06
DMWXCOS_0029 -6.084143918286966e-06 1 4.290266988427136e-06
Estimating the spectral parameters from the DMWaveX fit.
[16]:
# Get the Fourier amplitudes and powers and their uncertainties.
# Note that the `DMWaveX` amplitudes have the units of DM.
# We multiply them by a constant factor to convert them to dimensions
# of time so that they are consistent with `PLDMNoise`.
scale = DMconst / (1400 * u.MHz) ** 2
idxs = np.array(m2.components["DMWaveX"].get_indices())
a = np.array(
[(scale * m2[f"DMWXSIN_{idx:04d}"].quantity).to_value("s") for idx in idxs]
)
da = np.array(
[(scale * m2[f"DMWXSIN_{idx:04d}"].uncertainty).to_value("s") for idx in idxs]
)
b = np.array(
[(scale * m2[f"DMWXCOS_{idx:04d}"].quantity).to_value("s") for idx in idxs]
)
db = np.array(
[(scale * m2[f"DMWXCOS_{idx:04d}"].uncertainty).to_value("s") for idx in idxs]
)
print(len(idxs))
P = (a**2 + b**2) / 2
dP = ((a * da) ** 2 + (b * db) ** 2) ** 0.5
f0 = (1 / Tspan).to_value(u.Hz)
fyr = (1 / u.year).to_value(u.Hz)
29
[17]:
# We can create a `PLDMNoise` model from the `DMWaveX` model.
# This will estimate the spectral parameters from the `DMWaveX`
# amplitudes.
m3 = pldmnoise_from_dmwavex(m2)
print(m3)
# Created: 2024-04-26T18:15:16.781134
# PINT_version: 1.0
# User: docs
# Host: build-24199856-project-85767-nanograv-pint
# OS: Linux-5.19.0-1028-aws-x86_64-with-glibc2.35
# Python: 3.11.6 (main, Feb 1 2024, 16:47:41) [GCC 11.4.0]
# Format: pint
PSR SIM4
EPHEM DE440
CLOCK TT(BIPM2019)
UNITS TDB
START 53000.9999999566649306
FINISH 56985.0000000461960185
DILATEFREQ N
DMDATA N
NTOA 2000
CHI2 1857.424900754861
CHI2R 0.9599095094340367
TRES 0.97162572601109028586
RAJ 4:59:59.99999813 1 0.00000189187880060054
DECJ 15:00:00.00005795 1 0.00016094659501375309
PMRA 0.0
PMDEC 0.0
PX 0.0
F0 99.99999999999995441 1 3.6172376841794999413e-14
F1 -9.999997374756911203e-16 1 8.3063805585857470247e-22
PEPOCH 55000.0000000000000000
TZRMJD 55000.0000000000000000
TZRSITE gbt
TZRFRQ 1400.0
PHOFF 0.0008532562142660407 1 5.485044809139759e-06
TNDMAMP -13.077230959411352 0 0.04482343031374267
TNDMGAM 3.521026400935751 0 0.2376152092427078
TNDMC 29.0
PLANET_SHAPIRO N
DM 15.000002844181466291 1 4.9639686941126820373e-06
[18]:
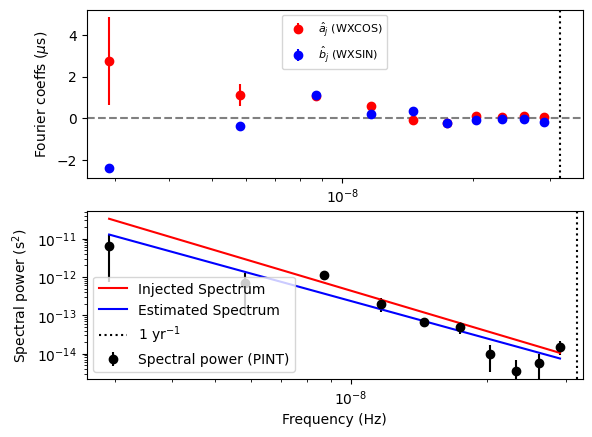
# Now let us plot the estimated spectrum with the injected
# spectrum.
plt.subplot(211)
plt.errorbar(
idxs * f0,
b * 1e6,
db * 1e6,
ls="",
marker="o",
label="$\\hat{a}_j$ (DMWXCOS)",
color="red",
)
plt.errorbar(
idxs * f0,
a * 1e6,
da * 1e6,
ls="",
marker="o",
label="$\\hat{b}_j$ (DMWXSIN)",
color="blue",
)
plt.axvline(fyr, color="black", ls="dotted")
plt.axhline(0, color="grey", ls="--")
plt.ylabel("Fourier coeffs ($\mu$s)")
plt.xscale("log")
plt.legend(fontsize=8)
plt.subplot(212)
plt.errorbar(
idxs * f0, P, dP, ls="", marker="o", label="Spectral power (PINT)", color="k"
)
P_inj = m.components["PLDMNoise"].get_noise_weights(t)[::2][:nharm_opt]
plt.plot(idxs * f0, P_inj, label="Injected Spectrum", color="r")
P_est = m3.components["PLDMNoise"].get_noise_weights(t)[::2][:nharm_opt]
print(len(idxs), len(P_est))
plt.plot(idxs * f0, P_est, label="Estimated Spectrum", color="b")
plt.xscale("log")
plt.yscale("log")
plt.ylabel("Spectral power (s$^2$)")
plt.xlabel("Frequency (Hz)")
plt.axvline(fyr, color="black", ls="dotted", label="1 yr$^{-1}$")
plt.legend()
29 29
[18]:
<matplotlib.legend.Legend at 0x7f8b027e83d0>