This Jupyter notebook can be downloaded from Wideband_TOA_walkthrough.ipynb, or viewed as a python script at Wideband_TOA_walkthrough.py.
Wideband TOA fitting
Traditional pulsar timing involved measuring only the arrival time of each pulse. But as receivers have covered wider and wider contiguous bandwidths, it became necessary to generate many TOAs for each time interval, covering different subbands. This frequency coverage allowed better handling of changing dispersion measures, but resulted in a large number of TOAs and had certain limitations. A new approach measures the pulse arrival time and the dispersion measure simultaneously from a frequency-resolved data cube. This produces TOAs, each of which has an associated dispersion measure and uncertainty. Working with this data requires different handling from PINT. This notebook demonstrates that.
[1]:
import astropy.units as u
import matplotlib.pyplot as plt
from astropy.visualization import quantity_support
from pint.fitter import Fitter
from pint.models import get_model_and_toas
import pint.config
import pint.logging
# setup logging
pint.logging.setup(level="INFO")
quantity_support()
[1]:
<astropy.visualization.units.quantity_support.<locals>.MplQuantityConverter at 0x7f93f35bc5d0>
Set up your inputs
[2]:
model, toas = get_model_and_toas(
pint.config.examplefile("J1614-2230_NANOGrav_12yv3.wb.gls.par"),
pint.config.examplefile("J1614-2230_NANOGrav_12yv3.wb.tim"),
)
The DM and its uncertainty are recorded as flags, pp_dm and pp_dme on the TOAs that have them, They are not currently available as Columns in the Astropy object. On the other hand, it is not necessary that every observation have a measured DM.
(The name, pp_dm, refers to the fact that they are obtained using “phase portraits”, like profiles but in one more dimension.)
[3]:
print(open(toas.filename).readlines()[-1])
guppi_57922_J1614-2230_0006.12y.x.ff 812.60505020 57922.064007172196642 0.419 gbt -pp_dm 34.4877666 -pp_dme 0.0004867 -be GUPPI -ver 20200204 -nchx 55 -tobs 891.204 -f Rcvr_800_GUPPI -gof 1.041 -snr 169.071 -fratio 1.258 -pta NANOGrav -subint 1 -nch 64 -flux 2.43148 -bw 187.435 -chbw 3.125 -fe Rcvr_800 -fluxe 0.01498 -nbin 2048 -proc 12y -tmplt J1614-2230.Rcvr_800.GUPPI.12y.x.avg_port.spl -flux_ref_freq 836.73551
[4]:
toas.table[-1]
[4]:
| index | mjd | mjd_float | error | freq | obs | flags | delta_pulse_number | tdb | tdbld | ssb_obs_pos | ssb_obs_vel | obs_sun_pos |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| d | us | MHz | km | km / s | km | |||||||
| int64 | object | float64 | float64 | float64 | str3 | object | float64 | object | float128 | float64[3] | float64[3] | float64[3] |
| 274 | 57922.06400717255 | 57922.06400717254 | 0.419 | 812.6050502 | gbt | {'format': 'Tempo2', 'name': 'guppi_57922_J1614-2230_0006.12y.x.ff', 'pp_dm': '34.4877666', 'pp_dme': '0.0004867', 'be': 'GUPPI', 'ver': '20200204', 'nchx': '55', 'tobs': '891.204', 'f': 'Rcvr_800_GUPPI', 'gof': '1.041', 'snr': '169.071', 'fratio': '1.258', 'pta': 'NANOGrav', 'subint': '1', 'nch': '64', 'flux': '2.43148', 'bw': '187.435', 'chbw': '3.125', 'fe': 'Rcvr_800', 'fluxe': '0.01498', 'nbin': '2048', 'proc': '12y', 'tmplt': 'J1614-2230.Rcvr_800.GUPPI.12y.x.avg_port.spl', 'flux_ref_freq': '836.73551', 'clkcorr': '3.023951845889943e-05'} | 0.0 | 57922.06480791843 | 57922.064807918432745 | -8106233.828294313 .. -60075124.09656769 | 29.431081448790245 .. -0.7083729035832717 | 8524988.622096533 .. 60354832.968297414 |
[5]:
toas.table["flags"][0]
[5]:
FlagDict({'format': 'Tempo2', 'name': '54724.000006.1.000.000.9y.x.ff', 'pp_dm': '34.4828090', 'pp_dme': '0.0118764', 'be': 'GASP', 'ver': '20200204', 'nchx': '16', 'tobs': '60.078', 'f': 'Rcvr_800_GASP', 'gof': '1.035', 'snr': '35.572', 'fratio': '1.073', 'pta': 'NANOGrav', 'subint': '0', 'nch': '16', 'bw': '60.000', 'chbw': '4.000', 'fe': 'Rcvr_800', 'nbin': '2048', 'proc': '12y', 'tmplt': 'J1614-2230.Rcvr_800.GUPPI.12y.x.avg_port.spl', 'to': '-8.970e-07', 'clkcorr': '2.6166525221999545e-05'})
Do the fit
As before, but now we need a fitter adapted to wideband TOAs. The function Fitter.auto() will examine the model and choose an appropriate one.
[6]:
fitter = Fitter.auto(toas, model)
[7]:
fitter.fit_toas()
[7]:
True
What is new, compared to narrowband fitting?
Residual objects combine TOA and time data
[8]:
type(fitter.resids)
[8]:
pint.residuals.WidebandTOAResiduals
If we look into the resids attribute, it has two independent Residual objects.
[9]:
fitter.resids.toa, fitter.resids.dm
[9]:
(<pint.residuals.Residuals at 0x7f93f27b29d0>,
<pint.residuals.WidebandDMResiduals at 0x7f93f27d17d0>)
Each of them can be used independently
Time residual
[10]:
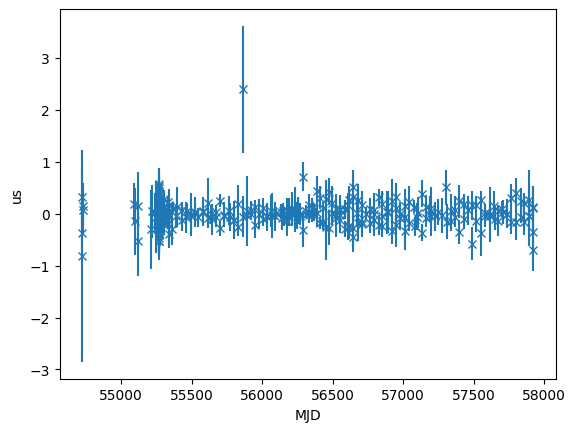
time_resids = fitter.resids.toa.time_resids
plt.errorbar(
toas.get_mjds().value,
time_resids.to_value(u.us),
yerr=toas.get_errors().to_value(u.us),
fmt="x",
)
plt.ylabel("us")
plt.xlabel("MJD")
[10]:
Text(0.5, 0, 'MJD')
[11]:
# Time RMS
print(fitter.resids.toa.rms_weighted())
print(fitter.resids.toa.chi2)
0.17493106055088772 us
156.75077380469221332
DM residual
[12]:
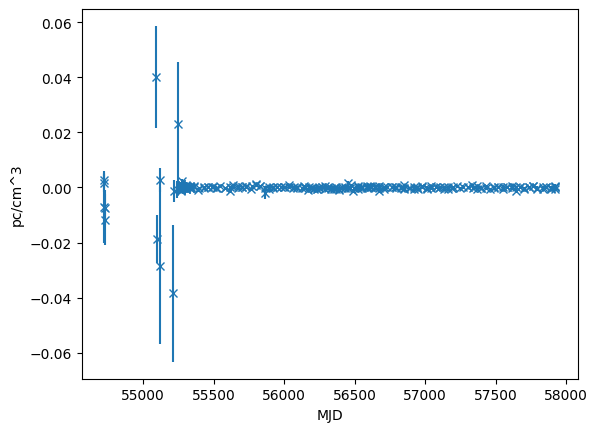
dm_resids = fitter.resids.dm.resids
dm_error = fitter.resids.dm.get_data_error()
plt.errorbar(toas.get_mjds().value, dm_resids.value, yerr=dm_error.value, fmt="x")
plt.ylabel("pc/cm^3")
plt.xlabel("MJD")
[12]:
Text(0.5, 0, 'MJD')
[13]:
# DM RMS
print(fitter.resids.dm.rms_weighted())
print(fitter.resids.dm.chi2)
0.00035817067609101146 pc / cm3
276.42008393172966
However, in the combined residuals, one can access rms and chi2 as well
[14]:
print(fitter.resids.rms_weighted())
print(fitter.resids.chi2)
{'toa': <Quantity 1.74931061e-07 s>, 'dm': <Quantity 0.00035817 pc / cm3>}
433.1708577364218541
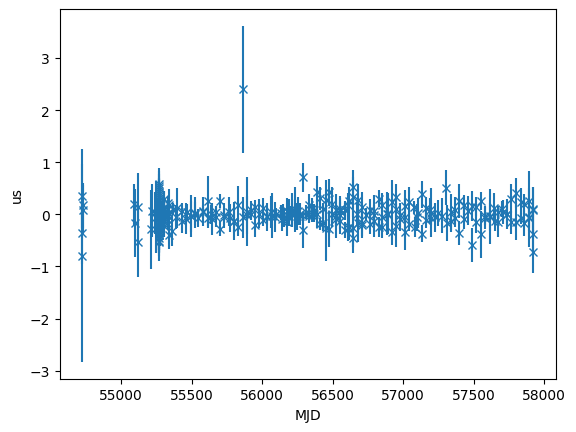
The initial residuals is also a combined residual object
[15]:
time_resids = fitter.resids_init.toa.time_resids
plt.errorbar(
toas.get_mjds().value,
time_resids.to_value(u.us),
yerr=toas.get_errors().to_value(u.us),
fmt="x",
)
plt.ylabel("us")
plt.xlabel("MJD")
[15]:
Text(0.5, 0, 'MJD')
[16]:
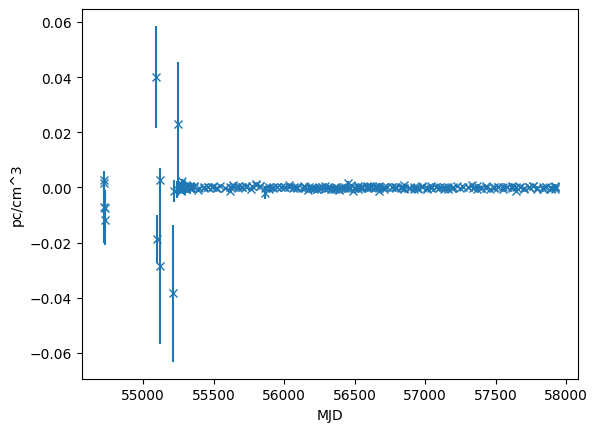
dm_resids = fitter.resids_init.dm.resids
dm_error = fitter.resids_init.dm.get_data_error()
plt.errorbar(toas.get_mjds().value, dm_resids.value, yerr=dm_error.value, fmt="x")
plt.ylabel("pc/cm^3")
plt.xlabel("MJD")
[16]:
Text(0.5, 0, 'MJD')
Matrices
We’re now fitting a mixed set of data, so the matrices used in fitting now have different units in different parts, and some care is needed to keep track of which part goes where.
Design Matrix are combined
[17]:
d_matrix, labels, units = fitter.get_designmatrix()
[18]:
print("Number of TOAs:", toas.ntoas)
print("Number of DM measurments:", len(fitter.resids.dm.dm_data))
print("Number of fit params:", len(fitter.model.free_params))
print("Shape of design matrix:", d_matrix.shape)
Number of TOAs: 275
Number of DM measurments: 275
Number of fit params: 130
Shape of design matrix: (275, 131)
Covariance Matrix are combined
[19]:
# c_matrix = fitter.get_noise_covariancematrix()
[20]:
# print("Shape of covariance matrix:", c_matrix.shape)
NOTE the matrix are PINTMatrix object right now, here are the difference
If you want to access the matrix data
[21]:
# print(d_matrix.matrix)
PINT matrix has labels that marks all the element in the matrix. It has the label name, index of range of the matrix, and the unit.
[22]:
# print("labels for dimension 0:", d_matrix.labels[0])
[ ]: